همانطور که از قبل به خاطر دارید در معادلات معمولی وقتی به همچین عبارتی می رسیدیم: 5x = 10 خیلی ساده میتوانستیم بنویسیم: x=2 اما در معادلات مثلثاتی داستان به این سادگی ها نیست! زیرا توابع مثلثاتی متناوبند.
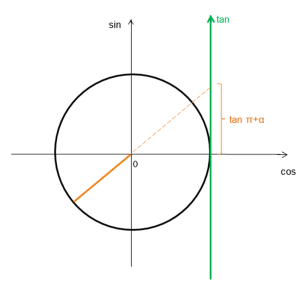
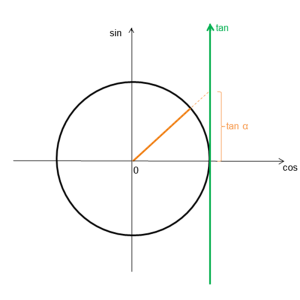
فرض کنید α یک عدد معلوم هست و x مجهول. اگر داشته باشیم: tan α = tan x آنگاه داریم: x=kπ+α. دقت کنید که در معادلات مثلثاتی از tan α = tan x نمی توان فقط نتیجه گرفت: x = α. به دلیل تناوبی بودن توابع مثلثاتی، باید نتیجه گرفت: x=kπ+α، که در آن k= 0, ±1, ±2, ±3. در حالتی که k=1 است، همانطور که در شکل زیر میبینید، تانژانت α با تانژانت π+α برابر است.
تانژانت α
 تانژانت π+α
تانژانت π+α
در حالت هایی که …,k=3, 5, 7 نیز حالت هایی شبیه اشکال بالا پیش می آید. ولی در حالت هایی که …,k=2, 4, 6 است، مانند این است که دارید دایره مثلثاتی را دور میزنید، در این حالت مقدار تانژانت تغییری نخواهد کرد. بنابراین کاملا درست است که از معادله tan α = tan x نتیجه بگیریم x=kπ+α.